🟉 Gradien Garis Singgung
Kurva di Suatu Titik
Diketahui fungsi y = f(x)
mempunyai turunan pada x = a. Turunan fungsi f(x) pada x = a atau f’(x) ditafsirkan secara geometris sebagai gradien garis singgung kurva di titik (a,
f(a)).
Jadi, gradien garis singgung kurva y = f(x) di (a,
f(a)) adalah
m = y' = f'(a)
🟉 Persamaan Garis
Singgung Kurva
Diketahui kurva y =
f(x) dan gradien di suatu titik (x₁, y₁) adalah m, maka
persamaan garis singgung di titik tersebut adalah
y - y₁ = m(x - x₁)
Contoh:
Jika diketahui kurva y = -2x3
+ 3x – 6, tentukan gradien dan persamaan garis singgung di titik dengan absis
-1!
Jawab:
Diketahui kurva y = -2x3
+ 3x – 6
x = -1 ⇒ y = -2x3 + 3x – 6
= -2(-1)3 + 3(-1) – 6
= -2(-1) – 3 – 6
= 2 – 3 – 6
= -7
sehingga diperoleh titik (-1,
-7)
m = y’ = -6x2 + 3
x = -1 ⇒ m = y’ = -6x2 + 3
= -6(-1)2 + 3
= -6(1) + 3
= -6 + 3
= -3
Persamaan garis singgung di
titik (-1, -7) dengan gradien -3:
y – y₁ = m(x – x₁)
y – (-7) = -3(x – (-1))
y + 7 = -3(x + 1)
y + 7 = -3x – 3
y + 7 + 3x + 3 = 0
3x + y + 10 = 0
Jadi, gradien garis dari kurva y = -2x3
+ 3x – 6 adalah -3 dan persamaan garis singgung kurva y = -2x3 + 3x
– 6 di titik dengan absis -1 adalah 3x + y + 10 = 0.
B. Fungsi Naik dan Fungsi Turun
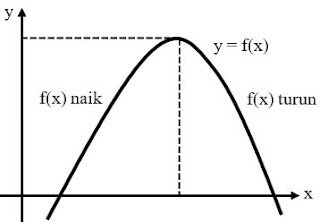
Perhatikan gambar
berikut!
- Fungsi f(x) dikatakan fungsi naik dalam interval l, jika untuk setiap x1 dan x2 dalam l dan x1 < x2, maka f(x1) < f(x2) atau dapat ditulis x1 < x2 ⇒ f(x1) < f(x2)
- Fungsi f(x) dikatakan fungsi turun dalam interval l, jika untuk setiap x1 dan x2 dalam l dan x1 < x2, maka f(x1) > f(x2) atau dapat ditulis x1 < x2 ⇒ f(x1) > f(x2)
🟉 Interval Fungsi Naik dan
Fungsi Turun
Suatu fungsi y = f(x)
berdasarkan teorema monoitas dapat ditentukan:
- Interval agar fungsi f(x) naik, syaratnya f’(x) > 0 (x < a atau x >b)
- Interval agar fungsi f(x) turun, syaratnya f’(x) < 0 (a < x < b)
- Apabila f’(x) = 0, maka fungsi dikatakan stasioner (tidak naik dan tidak turun)
Contoh:
Tentukan interval dari fungsi
y = x3 – 2x2 – 5 agar fungsi naik atau turun!
Jawab:
y = x3 – 2x2
– 5
y’ = 3x2 – 4x
3x2 – 4x = 0
x (3x – 4) = 0
x = 0 atau 3x – 4 = 0
3x = 4
x = 4/3
- Fungsi naik jika y’ > 0, maka intervalnya x < 0 atau x > 4/3
- Fungsi turun jika y’ < 0, maka intervalnya 0 < x < 4/3
Jadi, fungsi y = x3 – 2x2 – 5
naik untuk interval x < 0 atau x > 4/3 dan fungsi y = x3 – 2x2 –
5 turun untuk interval 0 < x < 4/3.
C. Nilai Stasioner
Apabila suatu fungsi y = f(x)
terdiferensial di x = a dengan f’(a) = 0, maka f(a) adalah nilai stasioner dari
fungsi f(x) di x = a. Titik stasioner adalah titik (a, f(a)) dengan x = a
diperoleh dari f’(x) = 0.
Contoh:
Tentukan nilai stasioner dan
titik stasioner dari kurva f(x) = 3x2 – 4x + 3!
Jawab:
f(x) = 3x2 – 4x + 3
f’(x) = 0
6x – 4 = 0
6x = 4
x = 4/6
x = 2/3
Diperoleh x = 2/3
f(x) = 3x2 – 4x + 3
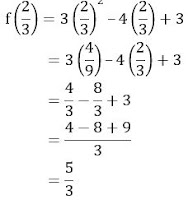
Jadi, nilai stasioner dari kurva f(x) = 3x2 – 4x + 3 adalah 5/3
f(x) = 3x2 – 4x + 3 adalah (2/3, 5/3)
D. Penerapan Turunan Fungsi dalam Pemecahan Materi
🟉 Perhitungan Kecepatan
dan Percepatan
Diketahui panjang
lintasan s sebagai fungsi waktu t ditentukan oleh s = f(t) dalam interval waktu
t.
Rumus:

Ket:
v(t) = kecepatan
s = panjang lintasan
a(t) = percepatan
t = waktu
Contoh:
Sebuah benda bergerak sepanjang lintasan (s) garis lurus. Panjang
lintasan s (dalam meter) pada waktu t detik dirumuskan s = f(t) = 2t3
– 5t2 + 10t – 6. Tentukan kecepatan dan percepatan benda ketika t =
5 detik!
Jawab:
s = f(t) = 2t3 – 5t2 + 10t – 6
▸ Kecepatan:
untuk t = 5,
didapat:
v(t) = 6t2 – 10t + 10
v(5) = 6(5)2 – 10(5) + 10
= 6(25) – 50 + 10
= 150 – 50 + 10
= 110
▸ Percepatan:
untuk t = 5,
didapat:
a(t) = 12t – 10
a(5) = 12(5) – 10
= 60 – 10
= 50
Jadi, kecepatan dan percepatan benda ketika t = 5
detik adalah 110 m/detik dan 50 meter/detik2.
🟉 Penyelesaian Masalah
yang Berkaitan dengan Nilai Ekstrim
Permasalahan yang berkaitan dengan nilai ekstrim suatu fungsi, antara
lain untuk menentukan luas terbesar, pengeluaran minimum, hasil kali terbesar,
dan lain sebagainya.
Langkah-langkah untuk menyelesaikan permasalahan yang berkaitan dengan
nilai ekstrim sebagai berikut:
- Membuat model matematika dari permasalahan
- Membuat rumusan fungsinya dalam satu variabel
- Menentukan penyelesaian optimumnya (maksimum atau minimum dari langkah kedua)
- Menafsirkan hasil yang diperoleh dari langkah ketiga
Contoh:
Suatu peluru ditembakkan ke
atas. Tinggi peluru pada t detik dirumuskan oleh h(t) = 40t – 5t2
(dalam meter). Tentukan tinggi maksimum yang dapat dicapai oleh peluru
tersebut!
Jawab:
Tinggi: h(t) = 40t – 5t2
Tinggi maksimum ketika h’(t) =
0, maka
h’(t) = 0
40 – 10t = 0
-10 t = -40
t = -40/-10
t = 4
h(4) = 40(4) – 5(4)2
= 160 – 5(16)
= 160 – 80
= 80
Jadi, tinggi maksimum peluru pada saat t = 4 detik
adalah 80 meter.
Semoga materi dan contoh soal tentang Karakteristik Grafik Fungsi ini bisa bermanfaat :)
Good luck guys~
No comments:
Post a Comment