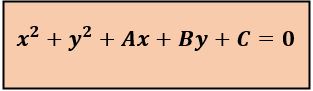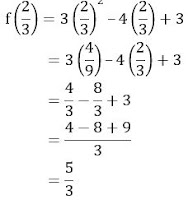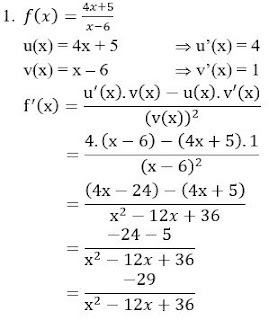KISI-KISI SOAL UJIAN SEMESTER GANJIL JENJANG SMK TAHUN PELAJARAN 2020/2021

Berikut adalah Kisi-Kisi Soal Ujian Semester Ganjil Jenjang SMK Tahun Pelajaran 2020/2021

☛ Kelas X

1. Siswa dapat menentukan hasil perkalian dari bilangan berpangkat
2. Siswa dapat menentukan hasil pembagian dari bilangan berpangkat
3. Siswa dapat menyederhanakan bilangan berpangkat ke dalam bentuk bilangan berpangkat positif
4. Siswa dapat menyatakan bilangan desimal ke dalam bentuk baku atau notasi ilmiah
5. Siswa dapat menyatakan bentuk baku atau notasi ilmiah ke dalam bilangan desimal
6. Siswa dapat menyederhanakan penjumlahan dan pengurangan bentuk akar
7. Siswa dapat menentukan hasil kali bentuk akar
8. Siswa dapat merasionalkan penyebut pecahan bentuk akar
9. Siswa dapat menentukan nilai dari operasi logaritma
10. Siswa dapat menentukan nilai dari persamaan logaritma sederhana
11. Siswa dapat menentukan hasil penyelesaian dari persamaan nilai mutlak
12. Siswa dapat menentukan hasil penyelesaian dari pertidaksamaan nilai mutlak
13. Siswa dapat menentukan himpunan penyelesaian dari sistem persamaan yang diketahui
14. Siswa dapat menentukan penyelesaian masalah yang berkaitan dengan SPLDV
15. Siswa dapat menentukan model matematika dari soal cerita yang diketahui
16. Siswa dapat menentukan penyelesaian masalah yang berkaitan dengan Program Linear

☛ Kelas XI

1. Siswa dapat menentukan himpunan penyelesaian dari persamaan kuadrat yang diketahui
2. Siswa dapat membentuk persamaan kuadrat jika diketahui dua persamaan linearnya
3. Siswa dapat menentukan jenis akar-akar persamaan kuadrat (nilai diskriminan)
4. Siswa dapat menentukan jumlah dan hasil kali akar-akar persamaan kuadrat
5. Siswa dapat menyusun persamaan kuadrat baru jika diketahui akar-akarnya
6. Siswa dapat menentukan sumbu simetri jika diketahui fungsi kuadratnya
7. Siswa dapat menentukan koordinat titik puncak jika diketahui fungsi kuadratnya
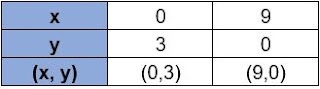
8. Siswa dapat menentukan persamaan fungsi kuadrat dari grafik fungsi yang diketahui
9. Siswa dapat menentukan tinggi maksimum sebuah benda (penerapan fungsi kuadrat)
10. Siswa dapat menentukan fungsi komposisi pada fungsi yang diketahui
11. Siswa dapat menentukan fungsi invers dari fungsi yang diketahui
12. Siswa dapat menentukan jari-jari lingkaran jika diketahui persamaan lingkarannya
13. Siswa dapat menentukan persamaan lingkaran jika diketahui jari-jarinya
14. Siswa dapat menentukan persamaan lingkaran jika diketahui titik-titiknya

☛ Kelas XII

1. Siswa dapat menentukan sampel dan populasi dari masalah yang diberikan
2. Siswa dapat menentukan tepi atas dan tepi bawah dari data kelompok yang diberikan
3. Siswa dapat menentukan rata-rata data tunggal
4. Siswa dapat menentukan rata-rata data kelompok
5. Siswa dapat menentukan median data tunggal
6. Siswa dapat menentukan median data kelompok
7. Siswa dapat menentukan modus data tunggal
8. Siswa dapat menentukan modus data kelompok
9. Siswa dapat menentukan jangkauan (range) dari data yang diberikan
10. Siswa dapat menentukan simpangan rata-rata dari data yang diberikan
11. Siswa dapat menentukan variansi dari data yang diberikan
12. Siswa dapat menentukan simpangan baku dari data yang diberikan
13. Siswa dapat menentukan nilai dari limit fungsi aljabar
14. Siswa dapat menentukan turunan dari fungsi aljabar
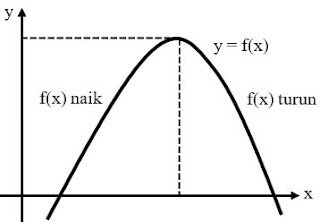
15. Siswa dapat menentukan interval grafik fungsi naik atau fungsi turun dari fungsi yang diketahui
16. Siswa dapat menyelesaikan permasalahan yang berkaitan dengan nilai ekstrim

Selamat berjuang, jangan lupa belajar dan berdoa.
Semoga hasil ujian memuaskan

Good luck guys~

PERSAMAAN LINGKARAN: Konsep Dasar, Penentuan Persamaan Lingkaran, Contoh Soal, dan Pembahasan

A.  KONSEP DASAR PERSAMAAN LINGKARAN

Lingkaran adalah tempat kedudukan atau himpunan titik-titik yang berjarak sama terhadap suatu titik yang tertentu. Titik tertentu tersebut dinamakan pusat lingkaran dan jarak yang tetap tersebut dinamakan jari-jari lingkaran.

Perhatikan lingkaran berikut!

Lingkaran tersebut dinamakan lingkaran P dan memiliki pusat di titik P(xp, yp). Panjang jari-jari lingkaran (r) menunjukkan jarak titik yang terletak pada lingkaran, sehingga PA = PB = r adalah jari-jari lingkaran.

1.  Rumus jarak (J) antara dua titik, yaitu titik A(x₁, y₁) dan B(x₂, y₂) sebagai berikut:

2.  Rumus jarak (J) titik A(x₁, y₁) ke garis ax + by + c = 0 sebagai berikut:

Rumus jarak tersebut dapat digunakan untuk menentukan persamaan sebuah lingkaran disesuaikan dengan variabel yang diketahui. 

B.  PENENTUAN PERSAMAAN LINGKARAN

☛  Penentuan Persamaan Lingkaran yang Berpusat di O(0,0) dengan jari-jari r

Lingkaran yang berpusat di titik pangkal, yaitu O(0,0). Titik A(x,y) terletak pada lingkaran. 

Berdasarkan rumus jarak antara dua titik, maka jarak titik O(0,0) ke titik A(x,y) sebagai berikut:

Persamaan lingkaran dengan pusat O(0,0) dan jari-jari r sebagai berikut:

Contoh 1:

Tentukan persamaan lingkaran yang berpusat di O(0,0) dengan jari-jari 3!

Jawab:

Titik pusat = (0,0) dan r = 3

x² + y² = r²

x² + y² = 3²

x² + y² = 9

Jadi, persamaan lingkaran tersebut adalah x² + y² = 9.

Contoh 2:

Tentukan titik pusat dan jari-jari pada lingkaran x² + y² = 16!

Jawab:

Persamaan lingkaran: x² + y² = 16

Titik pusat: (0,0)

Jari-jari: √16 = 4

Contoh 3:

Tentukan persamaan lingkaran yang berpusat pada pangkal koordinat dan melalui titik (5,12)!

Jawab:

Titik (5,12) terletak pada lingkaran.

Substitusikan (5,12) pada x² + y² = r²

  5² + 12² = r²

25 + 144 = r²

        169 = r²

Jadi, persamaan lingkaran yang berpusat pada pangkal koordinat dan melalui titik (5,12) adalah x² + y² = 169.

☛  Penentuan Persamaan Lingkaran yang Berpusat di P(xp, yp) dengan jari-jari r

Lingkaran yang berpusat di titik P(xp,yp). Titik A(x,y) terletak pada lingkaran.

Jarak antara titik P(xp,yp) terhadap titik A(x,y) sebagai berikut:

Persamaan lingkaran yang berpusat di P(xp,yp) dengan jari-jari r sebagai berikut:

Contoh 1:

Tentukan persamaan lingkaran yang berpusat di (2,-1) dengan jari-jari 3√2!

Jawab:

Persamaan lingkaran yang melalui pusat titik (xp,yp) adalah (x - xp)² + (y - yp)² = r².

Untuk lingkaran dengan pusat (2,-1) dan jari-jari 3√2, diperoleh:

(x - 2)² + (y - (-1))² = (3√2)²

(x - 2)² + (y + 1)² = 18

Jadi, persamaan lingkaran tersebut adalah (x - 2)² + (y + 1)² = 18.

Contoh 2:

Tentukan persamaan lingkaran yang berpusat di (4,5) dengan jari-jari 4!

Jawab:

Persamaan lingkaran yang melalui pusat titik (xp,yp) adalah (x - xp)² + (y - yp)² = r².

Untuk lingkaran dengan pusat (4,5) dan jari-jari 4, diperoleh:

(x - 4)² + (y - 5)² = 4²

(x - 4)² + (y - 5)² = 16

Jadi, persamaan lingkaran tersebut adalah (x - 4)² + (y - 5)² = 16.

Contoh 3:

Tentukan persamaan lingkaran jika suatu lingkaran berpusat di titik (-2,1) dan melalui titik (4,9)!

Jawab:

Jarak kedua titik merupakan jari-jari, maka:

r = √(x₂ - x₁)² + (y₂ - y₁)²

  = √(4 - (-2))² + (9 - 1)²

  = √(4 + 2)² + (9 - 1)²

  = √6² + 8²

  = √36 + 64

  = √100

  = 10

Persamaan lingkaran:

(x - xp)² + (y - yp)² = r²

(x - (-2))² + (y - 1)² = 10²

(x + 2)² + (y - 1)² = 100

Jadi, persamaan lingkaran tersebut adalah (x + 2)² + (y - 1)² = 100,

☛  Penentuan Bentuk Umum Persamaan Lingkaran

Bentuk persamaan lingkaran (x - xp)² + (y - yp)² = r² dapat dijabarkan menjadi suku-suku yang paling sederhana, sehingga diperoleh:

▸ Bentuk Umum Persamaan Lingkaran berikut:

dengan A = -2xp, B = -2yp dan C = xp² + yp² - r²

▸ Titik Pusat dan Jari-Jari Lingkaran dengan persamaan x² + y² + Ax + By + C = 0

sebagai berikut:

Contoh:

Tentukan titik pusat dan jari-jari lingkaran x² + y² + 4x - 6y - 12 = 0!

Jawab:

x² + y² + 4x - 6y - 12 = 0 ⇒ A = 4, B = -6, C = -12

Titik pusat = (-1/2.4 , -1/2.(-6))

                  = (-2, 3)

Jari-jari lingkaran:

r = √(1/2A)² + (1/2B)² - C

  = √(1/2.4)² + (1/2.(-6))² - (-12)

  = √2² + (-3)² + 12

  = √4 + 9 + 12

  = √25

  = 5

Jadi, titik pusat dan jari-jari lingkaran x² + y² + 4x - 6y - 12 = 0 adalah (-2, 3) dan 5.

LATIHAN SOAL!

1. Tentukan persamaan lingkaran yang berpusat di O(0,0) dengan jari-jari 6!
2. Tentukan titik pusat dan jari-jari pada lingkaran x² + y² = 64!
3. Tentukan persamaan lingkaran yang berpusat di (-7,3) dengan jari-jari 5!
4. Tentukan titik pusat dan jari-jari lingkaran x² + y² - 4x + 6y + 4 = 0!

Semoga materi dan contoh soal tentang Persamaan Lingkaran ini bisa bermanfaat :)

Good luck guys~

PROGRAM LINEAR: Pengertian, Model Matematika, Penyelesaian Masalah, Contoh Soal, dan Pembahasan

A.  PENGERTIAN PROGRAM LINEAR

Program linear adalah salah satu bidang matematika terapan yang banyak digunakan untuk memecahkan permasalahan yang melibatkan pembatasan suatu hal.

Contoh:

• Lowongan kerja mensyaratkan pelamar dengan batas pendidikan tertentu
• batas nilai cukup seorang pelajar agar dinyatakan lulus dari ujian
• batas berat badan seorang anak yang diperbolehkan menaiki suatu wahana permainan

Permasalahan program linear yaitu suatu permasalahan untuk menentukan besarnya masing-masing nilai variabel sedemikian rupa, sehingga nilai fungsi tujuan atau objektif yang linear menjadi optimum (maksimum atau minimum) dengan memerhatikan pembatasan yang ada. Agar masalah optimasi dapat diselesaikan dengan program linear, maka masalah tersebut harus diterjemahkan dalam bentuk model matematika.

B.  MODEL MATEMATIKA PADA PROGRAM LINEAR

Model matematika adalah suatu rumusan matematika (dapat berbentuk persamaan, pertidaksamaan, atau fungsi) yang diperoleh dari hasil penafsiran seseorang ketika menerjemahkan suatu masalah program linear ke dalam bahasa matematika. Suatu model matematika dikatakan baik apabila dalam model tersebut hanya memuat bagian-bagian yang perlu saja.

Untuk menyusun suatu model matematika dalam bentuk pertidaksamaan, diperlukan keterampilan memahami implikasi dari semua pernyataan yang memenuhi syarat-syarat tertentu.

Contoh:

Model matematika pada permasalahan program linear pada umunya membahas beberapa hal sebagai berikut:

1. Model matematika berbentuk sistem pertidaksamaan linear dua variabel yang merupakan bagian kendala-kendala yang harus dipenuhi oleh variabel itu sendiri.
2. Model matematika berkaitan dengan fungsi sasaran yang hendak dioptimalkan (minimalkan atau maksimalkan)

Contoh 1:

Seorang penjahit membuat model 2 model gorden. Model pertama memerlukan 1 meter kain polos dan 1,5 meter kain bercorak. Model kedua memerlukan 2 meter kain polos dan 0,5 meter kain bercorak. Ia memiliki persediaan 20 meter kain polos dan 10 meter kain bercorak. Jika penjahit tersebut dapat membuat x gorden model pertama dan y gorden model kedua, maka buatlah model matematika dari permasalahan tersebut!

Jawab:

☛ Misal : 

     banyak gorden model pertama = x potong

     banyak gorden model kedua = y potong

☛ Permasalahan tersebut dapat ditulis dalam bentuk tabel berikut:

☛ Model matematika:

• x + 2y ≤ 20
• 1,5x + 0,5y ≤ 10 ⇔ 15x + 5y ≤ 100 ⇔  3x + y ≤ 20
• Banyaknya gorden model pertama dan gorden model kedua tidak mungkin negatif, maka pertidaksamaannya: x ≥ 0 dan y ≥ 0

Jadi, model matematika dari permasalahan tersebut adalah x + 2y ≤ 20, 3x + y ≤ 20, x ≥ 0 dan y ≥ 0.

Contoh 2:

Sebuah perusahaan kue setiap hari memproduksi 2 jenis kue, yaitu donat dan serabi. Untuk membuat donat diperlukan 20 gram tepung terigu dan 10 gram gula, sedangkan untuk membuat serabi diperlukan 10 gram tepung terigu dan 10 gram gula. Setiap hari, perusahaan hanya menyediakan tepung terigu dan gula masing-masing tidak lebih dari 800 kg dan 500 kg. Jika setiap hari dibuat x donat dan y serabi, maka buatlah model matematika dari permasalahan tersebut!

Jawab:

☛ Misal : 

     banyak donat = x buah

     banyak serabi = y buah

☛ Permasalahan tersebut dapat ditulis dalam bentuk tabel berikut:

☛ Model matematika:

• 20x + 10y ≤ 800.000 ⇔ 2x + y ≤ 80.000
• 10x + 10y ≤ 500.000 ⇔ x + y ≤ 50.000
• Banyaknya donat dan serabi tidak mungkin negatif, maka pertidaksamaannya: x ≥ 0 dan y ≥ 0

Jadi, model matematika dari permasalahan tersebut adalah x + y ≤ 80.000, x + y ≤ 50.000, x ≥ 0 dan y ≥ 0.

C.  PENYELESAIAN MASALAH PROGRAM LINEAR

Dalam program linear, bentuk objektif atau fungsi objektif adalah bentuk atau fungsi f(x, y) = ax + by yang hendak dioptimumkan (dimaksimumkan atau diminimumkan). Nilai optimum bentuk objektif dapat ditentukan dengan metode uji titik pojok (titik sudut).

Langkah-langkah untuk menentukan nilai optimum fungsi objektif dengan menggunakan metode uji titik pojok adalah sebagai berikut:

1. Menentukan koordinat titik-titik sudut daerah penyelesaian dari pertidaksamaan tersebut
2. Menggambar daerah penyelesaian dari kendala-kendala dalam masalah program linear tersebut
3. Mensubstitusi koordinat setiap titik pojok ke dalam fungsi objektif
4. Membandingkan nilai-nilai fungsi objektif tersebut. Nilai terbesar berarti menunjukkan nilai maksimum dari fungsi f(x, y), sedangkan nilai terkecil menunjukkan nilai minimum dari fungsi f(x, y)

Contoh 1:

Suatu program linear dapat diterjemahkan ke dalam model matematika x + 3y ≤ 9; 2x + y ≤ 8; x ≥ 0; y ≥ 0; dan x, y ∈ R. Tentukan titik maksimum fungsi objektif f(x, y) = x + 2y dan nilai maksimumnya!

Penyelesaian:

☛ Titik potong terhadap sumbu x dan y:

▸ x + 3y ≤ 9

▸ 2x + y ≤ 8

☛ Grafik:

☛ Titik potong B:

x + 3y = 9 | x2 | 2x + 6y = 18

2x + y = 8 | x1 | 2x +   y =   8    -

                                  5y = 10

                                    y = 10/5

                                    y = 2

y = 2 ⇔   x + 3y = 9

              x + 3(2) = 9

                   x + 6 = 9

                         x = 9 - 6

                         x = 3

Koordinat titik potong adalah B(3, 2)

☛ Uji Titik Pojok:

Jadi, titik maksimum dari f(x, y) = x + 2y adalah 9, sedangkan nilai maksimumnya

adalah 7.

Contoh 2:

Seorang pedagang sandal memiliki modal lebih dari Rp800.000,00. Ia merencanakan membeli dua jenis sandal, yaitu sandal pria dan sandal wanita. Harga beli sandal pria Rp20.000,00 per pasang dan keuntungan dari penjualan sandal pria Rp6.000,00 per pasang, sedangkan harga beli sandal wanita Rp16.000,00 per pasang dan keuntungan dari penjualan sandal wanita Rp5.000,00 per pasang. Mengingat kapasitas kios, pedagang tersebut akan membeli sandal sebanyak-banyaknya 450 pasang. Tentukan banyaknya sandal pria dan sandal wanita yang harus dibeli agar mendapat keuntungan maksimum!

Penyelesaian:

Misal : 

     banyak sandal pria = x

     banyak sandal wanita = y

Permasalahan tersebut dapat ditulis dalam bentuk tabel berikut:

Model matematika:

• x + y ≤ 450
• 20.000x + 16.000y ≥ 800.000 ⇔ 5x + 4y ≥ 200
• x ≥ 0
• y ≥ 0
• Z = 6.000x + 5.000y

☛ Titik potong terhadap sumbu x dan y:

▸ x + y ≤ 450

▸ 5x + 4y ≥ 200

☛ Grafik:

 
☛ Uji Titik Pojok:

Jadi, banyaknya sandal pria yang harus dibeli pedagang tersebut agar mendapat keuntungan maksimum adalah 450 pasang dengan keuntungan sebesar Rp2.700.000,00. 

LATIHAN SOAL!

Sebuah adonan roti basah dibuat dengan 2 kg tepung terigu dan 2 kg gula. Sedangkan sebuah adonan roti kering dibuat menggunakan 1 kg tepung terigu dan 2 kg gula. Ibu memiliki persediaan tepung terigu sebanyak 6 kg dan gula sebanyak 10 kg. Setiap satu adonan kue basah dapat memberikan keuntungan Rp75.000,00 dan setiap adonan kue kering dapat memberikan keuntungan Rp60.000,00. Tentukan banyaknya kombinasi adonan roti yang dapat dibuat dan keuntungan maksimum yang diperoleh Ibu!

Semoga materi dan contoh soal tentang Program Linear ini bisa bermanfaat :)

Good luck guys~

PENERAPAN SISTEM PERSAMAAN LINEAR DUA VARIABEL (SPLDV)

A.  BENTUK UMUM SISTEM PERSAMAAN LINEAR DUA VARIABEL

Perhatikan bentuk-bentuk persamaan berikut!

• 2x + 2y = 14
• p + q + 3 = 10
• 8z - 3w = 7
• 6a + 3b = b + 5
• 12m - n = 32
• 2r - 5s = 10

Persamaan-persamaan tersebut memiliki dua variabel yang belum diketahui nilainya. Bentuk inilah yang dimaksud dengan Persamaan Linear Dua Variabel (PLDV).

Persamaan Linear Dua Variabel adalah persamaan yang hanya memiliki dua variabel dan masing-masing variabel berpangkat satu.

Sistem Persamaan Linear Dua Variabel (SPLDV) adalah dua persamaan linear dua variabel yang saling terkait.

Secara matematis, bentuk umum dari sistem persamaan linear dua variabel sebagai berikut:

a₁x + b₁y = c₁

a₂x + b₂y = c₂

Keterangan:

     a₁, b₁, c₁, a₂, b₂, c₂, x, dan y adalah bilangan-bilangan real

     x dan y disebut variabel

     a₁ dan a₂ disebut koefisien variabel x

     b₁ dan b₂ disebut koefisien variabel y 

     c₁ dan c₂ disebut konstanta

B.  PENYELESAIAN DARI SISTEM PERSAMAAN LINEAR DUA VARIABEL

Penyelesaian dari SPLDV dapat ditentukan dengan 4 metode, diantaranya:

▸ Metode Grafik

Metode grafik adalah metode menentukan penyelesaian SPLDV dengan menggambar pada koordinat Cartesius dan mencari titik potong. Himpunan penyelesaian adalah titik potong kedua garis tersebut.

Berikut penentuan banyaknya penyelesaian suatu SPLDV berdasarkan grafiknya.

1. Jika kedua garis berpotongan di satu titik, maka sistem persamaan tersebut memiliki satu penyelesaian
2. Jika garis-garisnya tidak berpotongan di satu titik tertentu, maka sistem persamaan tersebut tidak memiliki penyelesaian atau himpunan penyelesaiannya adalah himpunan kosong
3. Jika kedua garis berimpit, maka sistem persamaan tersebut memiliki tak hingga penyelesaian.

Contoh:

Tentukan himpunan penyelesaian dari SPLDV x + 4y = 12 dan x + y = 6 dengan menggunakan metode grafik!

Penyelesaian:

x + 4y = 12

x + y = 6

Grafik:

Setelah dibentuk grafik dari kedua garis, terlihat bahwa koordinat titik potong kedua grafik tersebut adalah (4, 2).

Penyelesaian dari SPLDV tersebut adalah x = 4 dan y = 2.

Jadi, himpunan penyelesaian dari SPLDV tersebut adalah {(4, 2)}.

▸ Metode Eliminasi

Metode eliminasi merupakan metode penyelesaian sistem persamaan linear dua variabel dengan cara menghilangkan salah satu variabel, sehingga dihasilkan sistem persamaan linear dengan jumlah variabel lebih sedikit.

Untuk mengeliminasi salah satu variabel perlu disamakan dahulu koefisien variabel yang akan dieliminasi.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan 2x - 3y = 1 dan 2x + y = 5 dengan menggunakan metode eliminasi!

Penyelesaian:

2x - 3y = 1        ...(1)

2x + y = 5         ...(2)

Koefisien variabel x pada kedua persamaan sudah sama, sehingga dapat langsung dieliminasi.

2x - 3y = 1

2x + y = 5    -

    -4 y = -4

        y = -4/-4

        y = 1

Untuk menentukan nilai x dengan mengeliminasi variabel y, koefisien variabel y disamakan terlebih dahulu.

2x - 3y = 1 | x1 | 2x - 3y = 1

2x + y = 5  | x3 | 6x + 3y = 15   +

                                   8x = 16

                                     x = 16/8

                                     x = 2

Jadi, himpunan penyelesaian dari sistem persamaan tersebut adalah {(2, 1)}.

▸ Metode Substitusi

Metode substitusi adalah metode mengganti variabel yang satu ke variabel yang lain. Caranya dengan menyatakan salah satu variabel yang sama dalam persamaan yang lain.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan x - y = -1 dan x + y = 5 dengan menggunakan metode substitusi!

Penyelesaian:

x - y = -1        ...(1)

x + y = 5        ...(2)

Persamaan (2) dapat diubah menjadi:

x + y = 5 ⇔ x = 5 - y        ...(3)

Substitusi persamaan (3) ke persamaan (1):

      x - y = -1

5 - y - y = -1

   5 - 2y = -1

       -2y = -1 - 5

       -2y = -6

          y = -6/-2

          y = 3

Substitusi y = 3 ke persamaan (3)

x = 5 - y

   = 5 - 3

   = 2

Jadi, himpunan penyelesaian dari sistem persamaan tersebut adalah {(2, 3)}.

▸ Metode Campuran

Penyelesaian sistem persamaan linear dengan metode gabungan merupakan penyelesaian dengan menggunakan metode eliminasi dan substitusi. Metode ini bisa dikerjakan dengan substitusi terlebih dahulu atau dengan eliminasi terlebih dahulu.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan 3a + 2b = 28 dan 2a - 3b = -3 dengan menggunakan metode campuran!

Penyelesaian:

3a + 2b = 28  | x2 | 6a + 4b = 56

2a - 3b = -3    | x3 | 6a - 9b = -9    -

                                     13b = 65

                                         b = 65/13

                                         b = 5

b = 5 ⇔    2a - 3b = -3

               2a - 3(5) = -3

                  2a - 15 = -3

                         2a = -3 + 15

                         2a = 12

                           a = 12/2

                           a = 6

Jadi, himpunan penyelesaian dari sistem persamaan tersebut adalah {(6, 5)}.

C.  PENYELESAIAN MASALAH YANG BERKAITAN DENGAN SPLDV

Langkah-langkah menyelesaikan permasalahan dalam kehidupan sehari-hari yang berkaitan dengan sistem persamaan linear dua variabel sebagai berikut:

1. Menentukan besaran yang dirancang sebagai variabel suatu sistem persamaan linear
2. Merumuskan sistem persamaan sebagai model matematika dari masalahnya
3. Menentukan penyelesaian model matematika yang telah dirumuskan
4. Menjawab masalah yang dipersoalkan

Contoh:

Pada sebuah pertunjukkan, harga satu tiket untuk dewasa dan satu tiket untuk pelajar Rp25.000,00. Sedangkan harga dua tiket untuk dewasa dan satu tiket untuk pelajar Rp40.000,00.

Tentukan:

a. Harga masing-masing untuk satu tiket

b. Harga untuk 5 tiket dewasa dan 2 tiket pelajar

Penyelesaian:

Misal:

   x = harga satu tiket untuk dewasa

   y = harga satu tiket untuk pelajar

Model matematika:

x + y = 25.000        ...(1)

2x + y = 40.000      ...(2)

Eliminasi variabel y:

x + y = 25.000

2x + y = 40.000   -

       -x = -15.000

        x = 15.000

Substitusi x = 15.000 ke persamaan (1)

         x + y = 25.000

15.000 + y = 25.000

               y = 25.000 - 15.000

               y = 10.000

Jadi, harga satu tiket untuk dewasa adalah Rp15.000,00 dan harga satu tiket untuk pelajar adalah Rp10.000,00.

Sedangkan, harga 5 tiket untuk dewasa dan 2 tiket untuk pelajar:

5x + 2y = 5(15.000) + 2(10.000)

             = 75.000 + 20.000

             = 95.000

Jadi, harga 5 tiket untuk dewasa dan 2 tiket untuk pelajar adalah Rp95.000,00.

Semoga materi dan contoh soal tentang Sistem Persamaan Linear Dua Variabel ini bisa bermanfaat :)

Good luck guys~

KARAKTERISTIK GRAFIK FUNGSI: Persamaan Garis Singgung Kurva, Fungsi Naik, Fungsi Turun, Nilai Stasioner, Penerapan Turunan

A.  Persamaan Garis Singgung Kurva

🟉  Gradien Garis Singgung Kurva di Suatu Titik

Diketahui fungsi y = f(x) mempunyai turunan pada x = a. Turunan fungsi f(x) pada x = a atau f’(x) ditafsirkan secara geometris sebagai gradien garis singgung kurva di titik (a, f(a)).

Jadi, gradien garis singgung kurva y = f(x) di (a, f(a)) adalah

m = y' = f'(a)

🟉  Persamaan Garis Singgung Kurva

Diketahui kurva y = f(x) dan gradien di suatu titik (x₁, y₁) adalah m, maka persamaan garis singgung di titik tersebut adalah

y - y₁ = m(x - x₁)

Contoh:

Jika diketahui kurva y = -2x³ + 3x – 6, tentukan gradien dan persamaan garis singgung di titik dengan absis -1!

Jawab:

Diketahui kurva y = -2x³ + 3x – 6

x = -1     ⇒ y = -2x³ + 3x – 6

                      = -2(-1)³ + 3(-1) – 6

                      = -2(-1) – 3 – 6

                      = 2 – 3 – 6

                      = -7

sehingga diperoleh titik (-1, -7)

m = y’ = -6x² + 3

x = -1     ⇒ m = y’ = -6x² + 3

                       = -6(-1)² + 3

                       = -6(1) + 3

                       = -6 + 3

                       = -3

Persamaan garis singgung di titik (-1, -7) dengan gradien -3:

             y – y₁ = m(x – x₁)

           y – (-7) = -3(x – (-1))

               y + 7 = -3(x + 1)

               y + 7 = -3x – 3

y + 7 + 3x + 3 = 0

    3x + y + 10 = 0

Jadi, gradien garis dari kurva y = -2x³ + 3x – 6 adalah -3 dan persamaan garis singgung kurva y = -2x³ + 3x – 6 di titik dengan absis -1 adalah 3x + y + 10 = 0.

B.  Fungsi Naik dan Fungsi Turun

Perhatikan gambar berikut!

Berdasarkan gambar di atas, dapat disimpulkan bahwa:

• Fungsi f(x) dikatakan fungsi naik dalam interval l, jika untuk setiap x₁ dan x₂ dalam l dan x₁ < x₂, maka f(x₁) < f(x₂) atau dapat ditulis x₁ < x₂ ⇒ f(x₁) < f(x₂)
• Fungsi f(x) dikatakan fungsi turun dalam interval l, jika untuk setiap x₁ dan x₂ dalam l dan x₁ < x₂, maka f(x₁) > f(x₂) atau dapat ditulis x₁ < x₂ ⇒ f(x₁) > f(x₂)

🟉  Interval Fungsi Naik dan Fungsi Turun

Suatu fungsi y = f(x) berdasarkan teorema monoitas dapat ditentukan:

• Interval agar fungsi f(x) naik, syaratnya f’(x) > 0 (x < a atau x >b)
• Interval agar fungsi f(x) turun, syaratnya f’(x) < 0 (a < x < b)
• Apabila f’(x) = 0, maka fungsi dikatakan stasioner (tidak naik dan tidak turun)

Contoh:

Tentukan interval dari fungsi y = x³ – 2x² – 5 agar fungsi naik atau turun!

Jawab:

 y = x³ – 2x² – 5

y’ = 3x² – 4x

3x² – 4x = 0

x (3x – 4) = 0

x = 0 atau 3x – 4 = 0

                       3x = 4

                         x = 4/3

• Fungsi naik jika y’ > 0, maka intervalnya x < 0 atau x > 4/3
• Fungsi turun jika y’ < 0, maka intervalnya 0 < x < 4/3

Jadi, fungsi y = x³ – 2x² – 5 naik untuk interval x < 0 atau x > 4/3 dan fungsi y = x³ – 2x² – 5 turun untuk interval 0 < x < 4/3.

C.  Nilai Stasioner

Apabila suatu fungsi y = f(x) terdiferensial di x = a dengan f’(a) = 0, maka f(a) adalah nilai stasioner dari fungsi f(x) di x = a. Titik stasioner adalah titik (a, f(a)) dengan x = a diperoleh dari f’(x) = 0.

Contoh:

Tentukan nilai stasioner dan titik stasioner dari kurva f(x) = 3x² – 4x + 3!

Jawab:

f(x) = 3x² – 4x + 3

f’(x) = 0

6x – 4 = 0

      6x = 4

        x = 4/6

        x = 2/3

Diperoleh x = 2/3, kemudian mencari nilai stasioner:

f(x) = 3x² – 4x + 3

Jadi, nilai stasioner dari kurva f(x) = 3x² – 4x + 3 adalah 5/3 dan titik stasioner dari kurva

f(x) = 3x² – 4x + 3 adalah (2/3, 5/3).

D.  Penerapan Turunan Fungsi dalam Pemecahan Materi

🟉  Perhitungan Kecepatan dan Percepatan

Diketahui panjang lintasan s sebagai fungsi waktu t ditentukan oleh s = f(t) dalam interval waktu t.

Rumus:

Ket:

     v(t) = kecepatan

     s = panjang lintasan

     a(t) = percepatan

     t = waktu

Contoh:

Sebuah benda bergerak sepanjang lintasan (s) garis lurus. Panjang lintasan s (dalam meter) pada waktu t detik dirumuskan s = f(t) = 2t³ – 5t² + 10t – 6. Tentukan kecepatan dan percepatan benda ketika t = 5 detik!

Jawab:

s = f(t) = 2t³ – 5t² + 10t – 6

▸ Kecepatan:

     untuk t = 5, didapat:

     v(t) = 6t² – 10t + 10

     v(5) = 6(5)² – 10(5) + 10

            = 6(25) – 50 + 10

            = 150 – 50 + 10

            = 110

▸ Percepatan:

     untuk t = 5, didapat:

     a(t) = 12t – 10

     a(5) = 12(5) – 10

            = 60 – 10

            = 50

Jadi, kecepatan dan percepatan benda ketika t = 5 detik adalah 110 m/detik dan 50 meter/detik².

🟉  Penyelesaian Masalah yang Berkaitan dengan Nilai Ekstrim

Permasalahan yang berkaitan dengan nilai ekstrim suatu fungsi, antara lain untuk menentukan luas terbesar, pengeluaran minimum, hasil kali terbesar, dan lain sebagainya.

Langkah-langkah untuk menyelesaikan permasalahan yang berkaitan dengan nilai ekstrim sebagai berikut:

1. Membuat model matematika dari permasalahan
2. Membuat rumusan fungsinya dalam satu variabel
3. Menentukan penyelesaian optimumnya (maksimum atau minimum dari langkah kedua)
4. Menafsirkan hasil yang diperoleh dari langkah ketiga

Contoh:

Suatu peluru ditembakkan ke atas. Tinggi peluru pada t detik dirumuskan oleh h(t) = 40t – 5t² (dalam meter). Tentukan tinggi maksimum yang dapat dicapai oleh peluru tersebut!

Jawab:

Tinggi: h(t) = 40t – 5t²

Tinggi maksimum ketika h’(t) = 0, maka

      h’(t) = 0

40 – 10t = 0

      -10 t = -40

            t = -40/-10

            t = 4

h(4) = 40(4) – 5(4)²

       = 160 – 5(16)

       = 160 – 80

       = 80

Jadi, tinggi maksimum peluru pada saat t = 4 detik adalah 80 meter.

Semoga materi dan contoh soal tentang Karakteristik Grafik Fungsi ini bisa bermanfaat :)

Good luck guys~

FUNGSI INVERS: Pengertian, Rumus, Contoh Soal, dan Pembahasan

A.  PENGERTIAN FUNGSI INVERS

Fungsi invers adalah pemetaan yang memiliki arah berlawanan dengan fungsinya. Misalkan f suatu fungsi yang memetakan himpunan A ke himpunan B sehingga setiap elemen a ∈ A mempunyai peta f(a) = b di himpunan B.

Jika fungsi f : A ➝ B yang mempunyai peta f(a)= b,

maka invers f adalah fungsi g : B ➝ A dengan peta g(b)= a.

Relasi f⁻¹ bukan merupakan fungsi, karena ada q elemen B yang mempunyai dua kawan berbeda, yaitu 3 dan 4 di dalam himpunan A. Hal ini disebabkan karena f fungsi yang tidak satu-satu. Sedangkan, relasi g⁻¹ merupakan fungsi pada himpunan B, karena setiap elemen di dalam B mempunyai tepat satu kawan dalam A.

Jika f adalah fungsi dari A ke B, maka f⁻¹ adalah fungsi invers f dari B ke A jika dan hanya jika f fungsi satu-satu (bijektif)

B.  RUMUS FUNGSI INVERS

Jika suatu fungsi mempunyai invers, maka fungsi invers tersebut dapat dicari dengan dua cara sebagai berikut:

1. Membalik arah panah fungsi semula, apabila diagram panahnya diketahui
2. Menggunakan prinsip bahwa jika y = f(x), maka x = f⁻¹ (y)

Langkah-langkah menentukan invers fungsi menggunakan prinsip bahwa jika y = f(x), maka x = f⁻¹ (y) sebagai berikut:

1. Nyatakan persamaan fungsinya y = f(x)
2. Carilah x dalam y, namakan persamaan tersebut dengan x = f⁻¹ (y)
3. Ganti x dengan y dan y dengan x sehingga menjadi y = f⁻¹ (x), yang merupakan fungsi invers dari f

Untuk beberapa bentuk fungsi, inversnya dapat ditentukan dengan rumus sebagai berikut:

Contoh:

Tentukan rumus invers dari fungsi:

1.  f(x) = 2x - 6

2.  g(x) = 5 - 1/3x

3.  f(x) = 2x/(x-1), f⁻¹ (-2)

4.  g(x) = x - 8/2x + 5, g⁻¹ (1)

Penyelesaian:

1.  f(x) = 2x - 6

     f⁻¹ (x) = (x - b)/a

                = (x - (-6))/2

                = (x + 6)/2

                = 1/2x + 3

2.  g(x) = 5 - 1/3x

     g⁻¹ (x) = (x - b)/a

                = (x - 5)/ -1/3

                = (3x - 15)/ -1

                = -3x + 15

3.  f(x) = 2x/(x-1), f⁻¹ (-2)

     f⁻¹ (x) = -dx +b/cx - a

                = -(-1)x + 0/x - 2

                = x/x-2

     f⁻¹ (x) = x/x-2

     f⁻¹ (-2) = -2/ -2 - 2

                 = -2/-4

                 = 1/2

4.  g(x) = x - 8/2x + 5, g⁻¹ (1)

     g⁻¹ (x) = -dx + b/cx - a

                = -5x + (-8) / 2x - 1

                = -5x - 8 / 2x - 1

     g⁻¹ (x) = -5x - 8 / 2x - 1

     g⁻¹ (1) = -5(1) - 8 / 2(1) - 1

                = -5 - 8 / 2 - 1

                = -13 / 1

                = -13

Semoga materi dan contoh soal tentang Fungsi Invers ini bisa bermanfaat :)

Good luck guys~

TURUNAN FUNGSI ALJABAR : Konsep, Jumlah dan Selisih, Hasil Kali, Hasil Bagi, Aturan Rantai

A.  KONSEP TURUNAN FUNGSI

Menghitung limit fungsi yang mengarah ke konsep turunan

Dari grafik di atas diperoleh:

B.  TURUNAN FUNGSI ALJABAR

1. Turunan Jumlah dan Selisih Dua Fungsi

Apabila f(x) = u(x) ± v(x) dengan u(x) dan v(x) adalah fungsi-fungsi yang memiliki turunan u’(x) dan v’(x), maka diperoleh:

Contoh:

Tentukan turunan dari fungsi:

1.   f(x) = 2x² + 5x – 6

2.   f(x) = x³ + 8x² – 5x + 2

Jawab:

1.  f(x) = 2x² + 5x – 6

    f’(x) = 4x + 5

2.  f(x) = x³ + 8x² – 5x + 2

    f’(x) = 3x² + 16x – 5

2. Turunan Hasil Kali Dua Fungsi

Apabila f(x) = u(x) . v(x) dengan u(x) dan v(x) adalah fungsi-fungsi yang memiliki turunan u’(x) dan v’(x), maka diperoleh:

Contoh:

Tentukan turunan dari fungsi:

1.   f(x) = (5x + 3)(x – 4)

2.   f(x) = (x² – 2)(2x + 3)

Jawab:

1.   f(x) = (5x + 3)(x – 4)

     misal:

     u(x) = 5x + 3             ⇒ u’(x) = 5

     v(x) = x – 4               ⇒ v’(x) = 1

     f’(x) = u’(x) . v(x) + u(x) . v’(x)

             = 5.(x – 4) + (5x + 3).1

             = 5x – 20 + 5x + 3

             = 10x – 17

2.   f(x) = (x² – 2)(2x + 3)

     u(x) = x² – 2              ⇒ u’(x) = 2x

     v(x) = 2x + 3             ⇒ v’(x) = 2

     f’(x) = u’(x) . v(x) + u(x) . v’(x)

              = 2x.(2x + 3) + (x² – 2).2

              = 4x² + 6x + 2x² – 4

              = 6x² + 6x – 4

3. Turunan Hasil Bagi Dua Fungsi

Apabila f(x) = u(x)/v(x) dengan v(x) ≠ 0 serta u(x) dan v(x) adalah fungsi yang memiliki turunan u’(x) dan v’(x), maka diperoleh:

Contoh:

Tentukan turunan dari fungsi:

Jawab:

4. Turunan Fungsi f(x) = (u(x))ⁿ

Apabila f(x) = (u(x))ⁿ dengan u(x) adalah fungsi dari x yang memiliki turunan u’(x) dan n adalah bilangan real, maka diperoleh:

Contoh:

Tentukan turunan dari fungsi:

1.   f(x) = (2x – 8)³

2.   f(x) = 3(x² + 2)³

3.   f(x) = (5x² – 3)⁷

Jawab:

1.   f(x) = (2x – 8)³

     f’(x) = 3.(2x – 8)².2

             = 6(2x – 8)²

             = 6(4x² – 32x + 64)

             = 24x² – 192x + 384

2.   f(x) = 3(x² + 2)³

     f’(x) = 3.3(x² + 2)².(2x)

              = 18x(x⁴ + 4x² + 4)

              = 18x⁵ + 72x³ + 72x

3.   f(x) = (5x² – 3)⁷

     f’(x) = 7. (5x² – 3)⁶.10x

             = 70x (5x² – 3)⁶

5. Turunan dengan Aturan Rantai

Apabila y = (f(x))ⁿ, maka dy/dx atau apabila y = g(u), u = f(v), dan v = h(x), maka diperoleh:

Contoh:

Tentukan dy/dx dari fungsi y = (2x² – 4x - 3)³!

Jawab:

6. Turunan ke-n dari Suatu Fungsi

Suatu fungsi y = f(x) mempunyai turunan sebagai berikut:

Contoh:

Tentukan turunan ketiga dari fungsi f(x) = 5x⁵ – 4x³ + 7x – 8!

Jawab:

f(x) = 5x⁵ – 4x³ + 7x – 8

Turunan pertama           : f’(x) = 10x⁴ – 12x² + 7

Turunan kedua              : f”(x) = 40x³ – 24x

Turunan ketiga              : f’’’(x) = 120x² – 24

Jadi, turunan ketiga dari fungsi f(x) = 5x⁵ – 4x³ + 7x – 8 adalah 120x² – 24.

Semoga materi dan contoh soal tentang Turunan Fungsi Aljabar ini bisa bermanfaat :)

Good luck guys~