Bentuk umum dari fungsi kuadrat adalah sebagai berikut:
f(x) = y = ax² + bx + c
dengan syarat a, b, c ∈ R dan a ≠ 0.
Untuk syarat a ≠ 0 menjamin bahwa f(x) = y = ax² + bx + c bukan fungsi linear.
B. Sifat Grafik Fungsi Kuadrat
Fungsi kuadrat dapat digambarkan dalam bentuk grafik atau kurva yang berupa parabola.
Sifat-sifat grafik fungsi kuadrat adalah sebagai berikut:
- Jika a > 0, maka grafik terbuka ke atas dan mempunyai titik balik minimum.
- Jika a < 0, maka grafik terbuka ke bawah dan mempunyai titik balik maksimum.
- Jika D > 0, maka grafik memotong sumbu x di dua titik yang berbeda.
- Jika D = 0, maka grafik memotong sumbu x di satu titik atau menyinggung sumbu x.
- Jika D < 0, maka grafik tidak memotong sumbu x.
- Definit positif
Fungsi akan selalu bernilai positif untuk setiap x atau grafik fungsi kuadrat seluruhnya berada di atas sumbu x dengan syarat a > 0 dan D < 0.
- Definit Negatif
Fungsi akan selalu bernilai negatif untuk setiap x atau grafik fungsi kuadrat seluruhnya berada di bawah sumbu x dengan syarat a < 0 dan D < 0.
Agar lebih memahami mengenai bentuk grafik fungsi kuadrat, perhatikan gambar berikut:

Contoh:
Diketahui fungsi kuadrat f(x) = x² + 3mx + (4m + 1). Tentukan batas-batas nilai m agar grafik fungsi f(x) memotong sumbu x di dua titik yang berbeda!
Penyelesaian:
Fungsi kuadrat f(x) = x² + 3mx + (4m + 1)
didapat a = 1
b = 3m
c = (4m + 1)
Agar grafik fungsi f(x) memotong sumbu x di dua titik yang berbeda,
maka syaratnya : D > 0
sehingga:
D > 0
b² - 4ac > 0
(3m)² - 4.1.(4m + 1) > 0
9m² - 16m - 4 > 0
9m² - 18m + 2m - 4 > 0
9m (m - 2) + 2 (m - 2) > 0
(9m + 2) (m - 2) > 0
9m + 2 = 0 atau m - 2 = 0
9m = -2 m = 2
m = -2/9
Jadi, batas-batas nilai m yang memenuhi agar grafik fungsi f(x) memotong sumbu x di dua titik yang berbeda adalah m < -2/9 atau m > 2.
C. Menggambar Grafik Fungsi Kuadrat
Grafik fungsi kuadrat y = ax² + bx + c memiliki sumbu simetri, nilai ekstrim, dan titik puncak.
- Sumbu Simetri
Sumbu simetri adalah garis yang membagi grafik fungsi kuadrat menjadi dua bagian yang sama (simetris), yaitu dengan persamaan:
- Nilai Ekstrim
Nilai ekstrim fungsi kuadrat terdiri dari nilai maksimum dan nilai minimum. Nilai ekstrim juga bisa disebut dengan nilai optimum.
Nilai ekstrim fungsi kuadrat dapat dicari dengan:
- Koordinat Titik Puncak
Koordinat titik puncak grafik fungsi kuadrat adalah
Berikut adalah langkah-langkah menggambar grafik fungsi kuadrat:
- Menentukan titik potong grafik dengan sumbu koordinat. Titik potong grafik terhadap sumbu x, ketika y = 0. Titik potong grafik terhadap sumbu y, ketika x = 0.
- Menentukan sumbu simetri.
- Menentukan titik ekstrim atau nilai optimum.
- Menentukan koordinat titik puncak.
- Menghubungkan titik-titik yang diletakkan pada Koordinat Cartesius sehingga membentuk parabola atau kurva.
Gambarlah grafik fungsi kuadrat y = x² - 6x + 5!
Penyelesaian:
Fungsi kuadrat y = x² - 6x + 5
didapat a = 1
b = -6
c = 5
⋆ Menentukan titik potong grafik dengan sumbu koordinat
- Titik potong terhadap sumbu x (y = 0)
x² - 6x + 5 = 0
x² - 5x - x + 5 = 0
x(x - 5) - (x - 5) = 0
(x - 1)(x - 5) = 0
x - 1 = 0 atau x - 5 = 0
x = 1 x = 5
Diperoleh titik potong (1, 0) dan (5, 0)
- Titik potong terhadap sumbu y (x = 0)
y = x² - 6x + 5
y = 0² - 6(0) + 5
y = 0 - 0 + 5
y = 5
Diperoleh titik potong (0, 5)
⋆ Menentukan sumbu simetri
x = -b/2a
= -(-6)/2.1
= 6/2
= 3
Sumbu simetri: x = 3
⋆ Menentukan titik ekstrim atau nilai optimum
D = b² - 4ac
= (-6)² - 4.1.5
= 36 - 20
= 16
y = D/-4a
= 16/-4.1
= 16/-4
= -4
Titik ekstrim: y = -4
⋆ Menentukan koordinat titik puncak
Koordinat titik puncak = (x, y)
= (-b/2a , D/-4a)
= (3, -4)
⋆ Grafik fungsi kuadrat:

Semoga materi dan contoh soal tentang Fungsi Kuadrat ini bisa bermanfaat :)
Good luck guys~
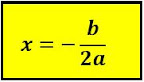


DEKE BAGASKARA XII TP1
ReplyDeleteNAMA: ACH RIYADDUS S
ReplyDeleteKLS: XI TKR 1
NO ABSEN : 04
Nama:Deny Firman s.b
ReplyDeleteKelas:XI TKR 2
Nama:Imam muntholib
ReplyDeleteKelas:XI TKR2
Nama:SITI AISAH
ReplyDeleteKelas:XI TKJ 2
Nama: Martha Rahayu Pandango
ReplyDeleteKelas: XI TKJ 2
Nama : ANITA YULANDIKA K.P.
ReplyDeleteKelas : XI TKJ 2
Nama: DWI DAMARA AGASTA
ReplyDeleteKls:11 TKJ 2
Nama :Sih panrimo adi
ReplyDeleteKls :xi Tkj 2
Nama: habibah eka k.
ReplyDeleteKelas: XI TKJ 2
Nama:Ari Ferdyansyah
ReplyDeleteKelas:XI TKJ 2
NAMA:IIK KUMBINASARI
ReplyDeleteKELAS:X TKJ2
Nama M SOFYAN
ReplyDeleteKks 11 TKR 3
Nama petrus arif bawono
ReplyDeleteKelas 11 tkj 2
Nama: Lailatul Fitria
ReplyDeleteKelas:XI TKJ2
Nama:FIRMANSAH
ReplyDeleteKelas:XI Tokr 2