A. JANGKAUAN (RANGE)
Jangkauan adalah selisih antara data terbesar dengan data terkecil.
- Jangkauan (Range) Data Tunggal
Untuk data tunggal, jangkauan dirumuskan:
J = Xmaks - Xmin
Contoh:
Tentukan range dari data: 6 10 20 15 3 7 5 8 3 7 9!
Jawab:
Xmaks = 20
Xmin = 3
J = Xmaks - Xmin
= 20 - 3
= 17
Jadi, range dari data tersebut adalah 17.
- Jangkauan (Range) Data Kelompok
Untuk data kelompok, nilai tertinggi diambil dari nilai tengah kelas tertinggi dan nilai terendah diambil dari nilai tengah kelas terendah. Jangkauan dirumuskan:
J = Nilai tengah kelas tertinggi - Nilai tengah kelas terendah
Contoh:
Perhatikan tabel berikut!
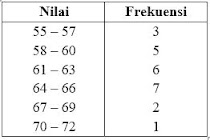
Tentukan range dari data di atas!
Jawab:

Tabel tersebut menunjukkan data dari 24 orang.
Nilai tengah kelas tertinggi adalah 71 dan nilai tengah kelas terendah adalah 56, maka
J = nilai tengah kelas tertinggi - nilai tengah kelas terendah
= 71 - 56
= 15
Jadi, range dari data tersebut adalah 15.
B. SIMPANGAN RATA-RATA
Simpangan rata-rata adalah ukuran yang menyatakan seberapa besar penyebaran tiap nilai data terhadap nilai rata-ratanya.
- Simpangan Rata-Rata Data Tunggal
Untuk data tunggal, simpangan rata-rata dapat dirumuskan:

Keterangan:
SR = Simpangan rata-rata
n = banyaknya data
xᵢ = data ke-i
i = 1, 2, 3, ..., n
x = rata-rata (mean)
Contoh:
Tentukan simpangan rata-rata dari data: 30 40 50 60 70!
Jawab:
Menentukan rata-rata terlebih dahulu:
Setelah menentukan rata-rata, selanjutnya simpangan rata-rata dapat ditentukan dengan rumus sebagai berikut:

Jadi, simpangan rata-rata dari data tersebut adalah 12.
- Simpangan Rata-Rata Data Kelompok
Untuk data kelompok atau data dari tabel distribusi frekuensi, simpangan rata-rata dapat dirumuskan:

Keterangan:
SR = Simpangan rata-rata
n = banyaknya data
fᵢ = frekuensi data ke-i
xᵢ = data ke-i
i = 1, 2, 3, ..., n
x = rata-rata (mean)
Contoh:
Tentukan simpangan rata-rata dari tabel berikut:

Jawab:

Menentukan rata-rata terlebih dahulu:
Setelah menentukan rata-rata, selanjutnya dari tabel tersebut, simpangan rata-rata dapat ditentukan dengan rumus sebagai berikut:

Jadi, simpangan rata-rata dari tabel tersebut adalah 0,768.
C. VARIANSI (RAGAM)
Variansi (Ragam) adalah rata-rata dari jumlah kuadrat simpangan tiap data.
- Variansi (Ragam) Data Tunggal
Untuk data tunggal, variansi (ragam) dapat dirumuskan:

Keterangan:
S² = variansi (ragam)
n = banyaknya data
xᵢ = data ke-i
i = 1, 2, 3, ..., n
x = rata-rata (mean)
- Variansi (Ragam) Data Kelompok
Untuk data kelompok, variansi (ragam) dapat dirumuskan:
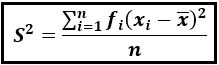
Keterangan:
S² = variansi (ragam)
n = banyaknya data
fᵢ = frekuensi data ke-i
xᵢ = data ke-i
i = 1, 2, 3, ..., n
x = rata-rata (mean)
D. SIMPANGAN BAKU (STANDART DEVIASI)
Simpangan Baku (Standart Deviasi) adalah nilai akar dari variansi (ragam).
- Simpangan Baku (Standart Deviasi) Data Tunggal
Untuk data tunggal, simpangan baku (standart deviasi) dapat dirumuskan:

Keterangan:
S = simpangan baku (standart deviasi)
n = banyaknya data
xᵢ = data ke-i
i = 1, 2, 3, ..., n
x = rata-rata (mean)
- Simpangan Baku (Standart Deviasi) Data Kelompok
Untuk data kelompok, simpangan baku (standart deviasi) dapat dirumuskan:

Keterangan:
S = simpangan baku (standart deviasi)
n = banyaknya data
fᵢ = frekuensi data ke-i
xᵢ = data ke-i
i = 1, 2, 3, ..., n
x = rata-rata (mean)
Contoh 1:
Tentukan variansi dan simpangan baku dari data 4 5 6 7 8!
Jawab:
Menentukan rata-rata terlebih dahulu:
Setelah menentukan rata-rata, selanjutnya variansi dan simpangan baku dapat ditentukan dengan rumus sebagai berikut:
⋆ Variansi

⋆ Simpangan Baku
S = √S²
= √2
Jadi, variansi dan simpangan baku dari data tersebut adalah 2 dan √2.
Contoh 2:
Perhatikan tabel distribusi frekuensi berikut!

Tentukan variansi dan simpangan baku dari tabel distribusi frekuensi di atas!
Jawab:

Menentukan rata-rata terlebih dahulu:
Setelah menentukan rata-rata, selanjutnya dari tabel tersebut, variansi dan simpangan baku dapat ditentukan dengan rumus sebagai berikut:
⋆ Variansi
⋆ Simpangan Baku
S = √S²
= √94,75
= 9,73
Jadi, variansi dan simpangan baku dari tabel tersebut adalah 94,75 dan 9,73.
Semoga materi dan contoh soal tentang Ukuran Penyebaran ini bisa bermanfaat :)
Good luck guys ~
DAVID SUGIYANTO XII TP 1
ReplyDeleteANDRE NATHAN XII LISTRIK
ReplyDeleteABDULLAH FAQIH RAMADHAN XII TP 1
ReplyDeleteM. Faris Hidayatullah. T XII TKRO 2
ReplyDeleteAchmad Khoirun Naja XII TP 1
ReplyDeleteAgung Sugiantoro Xll Tp1
ReplyDeleteFebrian Maulana XII Tp1
ReplyDeleteAditia hermawan XII TP 1
ReplyDelete