Refleksi (Pencerminan) merupakan suatu transformasi
yang memindahkan suatu titik pada bangun geometri dengan menggunakan sifat
benda dan bayangan pada cermin datar.
Rumus Refleksi (Pencerminan)
1. Pencerminan terhadap sumbu x
 2. Pencerminan terhadap sumbu y
2. Pencerminan terhadap sumbu y

3. Pencerminan terhadap titik asal O(0,0)

4. Pencerminan terhadap garis y = x

5. Pencerminan terhadap garis y = -x

6. Pencerminan terhadap garis x = h

7. Pencerminan terhadap garis y = k

8. Pencerminan terhadap titik (a,b)

Contoh:
Tentukan bayangan dari:
1. Titik A(-5, 3) jika direfleksikan terhadap sumbu x
2. Titik B(-4, -7) jika direfleksikan terhadap sumbu y
3. Titik C(-8, 2) jika direfleksikan terhadap titik asal
4. Titik D(10, -3) jika direfleksikan terhadap garis y = x
5. Titik E(9, -2) jika direfleksikan terhadap garis y = -x
6. Titik F(1, 3) jika direfleksikan terhadap garis x = -2
7. Garis 2x – y + 5 = 0 jika direfleksikan terhadap garis y = 2
8. Titik G(4, 6) jika direfleksikan terhadap titik (1, 2)
Jawab:


LATIHAN SOAL!!!
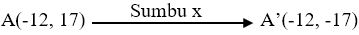 b) Direfleksikan terhadap sumbu y
b) Direfleksikan terhadap sumbu y
 c) Direfleksikan terhadap titik asal
c) Direfleksikan terhadap titik asal
 d) Direfleksikan terhadap garis y = x
d) Direfleksikan terhadap garis y = x




1. Pencerminan terhadap sumbu x


3. Pencerminan terhadap titik asal O(0,0)

4. Pencerminan terhadap garis y = x

5. Pencerminan terhadap garis y = -x

6. Pencerminan terhadap garis x = h

7. Pencerminan terhadap garis y = k

8. Pencerminan terhadap titik (a,b)

Contoh:
Tentukan bayangan dari:
1. Titik A(-5, 3) jika direfleksikan terhadap sumbu x
2. Titik B(-4, -7) jika direfleksikan terhadap sumbu y
3. Titik C(-8, 2) jika direfleksikan terhadap titik asal
4. Titik D(10, -3) jika direfleksikan terhadap garis y = x
5. Titik E(9, -2) jika direfleksikan terhadap garis y = -x
6. Titik F(1, 3) jika direfleksikan terhadap garis x = -2
7. Garis 2x – y + 5 = 0 jika direfleksikan terhadap garis y = 2
8. Titik G(4, 6) jika direfleksikan terhadap titik (1, 2)
Jawab:


LATIHAN SOAL!!!
1.
Tentukan
bayangan dari titik A(-12, 17) jika:
a)
Direfleksikan
terhadap sumbu x
b)
Direfleksikan
terhadap sumbu y
c)
Direfleksikan
terhadap titik asal
d)
Direfleksikan
terhadap garis y = x
e)
Direfleksikan
terhadap garis y = -x
f)
Direfleksikan
terhadap garis x = -5
g)
Direfleksikan
terhadap titik (3, -4)
2.
Tentukan
bayangan garis 3x – 2y + 6 =
0 jika direfleksikan terhadap garis y = -4!
Penyelesaian:
1. Bayangan dari titik A(-12, 17)
a) Direfleksikan terhadap sumbu x
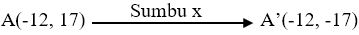



e) Direfleksikan terhadap garis y = -x

f) Direfleksikan terhadap garis x = -5

Titik
bayangan A’(2h - x,y)
didapat:
> x’
= 2h – x
> y’
= y
maka:
> x’
= 2(-5) – (-12) = -10 + 12 = 2
> y’
= 17
Jadi,
bayangan titik A(-12, 17) adalah A’(2, 17).
g) Direfleksikan terhadap titik (3, -4)

Titik
bayangan G’(2a - x, 2b - y)
didapat:
> x’
= 2a - x
> y’
= 2b - y
maka:
> x’
= 2(3) – (-12) = 6 + 12 = 18
> y’
= 2(-4) – 17 = -8 – 17 = -25
Jadi,
bayangan titik A(-12, 17) adalah A’(18, -25).
2. Bayangan garis 3x – 2y + 6 = 0 jika
direfleksikan terhadap garis y = -4

Titik
bayangan (x, 2k - y)
didapat:
> x’
= x
> y’
= 2k – y
maka:
> x’
= x « x = x’
> y’
= 2(-4) – y = -8 – y « y = -8 – y’
Substitusi ke persamaan:
3x – 2y + 6 = 0
3(x’) – 2(-8 – y’) + 6 = 0
3x’ + 16 + 2y’ + 6 = 0
3x’ + 2y’ + 22 = 0
Jadi, bayangan garis 3x – 2y + 6 = 0 adalah 3x + 2y + 22 = 0.
Semoga materi, contoh soal, dan latihan soal tentang Refleksi (Pencerminan) ini bisa bermanfaat :)
Pelajari materi Rotasi (Perputaran) disini!
Good luck guys~
Terimakasih kak, sangat membantu :)
ReplyDeleteKalau bisa, dilengkapi contoh soal jg ya kak..
Iya kak, ini blog juga masih baru. Nanti insyaallah pasti diberi latihan soal.
DeleteMakasih sarannya kak :)
NAMA:FADLI AS'AD FAWAID
ReplyDeleteKLS:XI TP1
Terimakasih :)
DeleteNama:Ersal syahreza
ReplyDeleteKelas:XI Tp1
Terimakasih :)
DeleteNama:Ersal syahreza
ReplyDeleteKelas:XI Tp1
Nama :MUHAMMAD ARIFIN KOHAR
ReplyDeleteKelas :XI TP2
Nama :NUR WAHYUDI
ReplyDeleteKelas:XI TP3
Nama : MOCH. ARIFIN ILHAM
ReplyDeleteKelas: XI TP2
Nama : MOCH. ARIFIN ILHAM
ReplyDeleteKelas: XI TP2
Nama:Andre Maulana Fahmi
ReplyDeleteKls : XI Tp1
ABS : 17
Nama:Ahmad zaelani
ReplyDeleteKelas:XI Tp1
Nama:Aldi andrian
ReplyDeletekelas:Xl Tp 1
Lukman nur hakim XII TKR 2
ReplyDelete